Click here for Wednesday May 1 sprint 17688.
Problem 1:
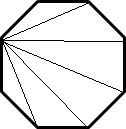
The sum of the angles in a triangle = 180 degrees or:
`180 = \alpha + \beta +\gamma`
Multiply 180 by 6 triangles to get the total sum of all theangles
`6 * 180 = 1080`
So the interior angles of a hexagon add to `1080` degrees.
The problem supplies 3 angles and asks for the value of one of the equal sized remaining angles. An octagon has 8 interior angles so 8-3 = 5 meaning there are 5 equal sized angles plus the three given that add to 1080 degrees.
`1080 = 64 + 41 + 40 + x + x + x + x + x`
`1080 = 145 + 5x`
`1080 - 145 = 1080 - 145 + 2x`
`935 = 5x`
`935/5 = (5x)/5`
`187 = x`
Problem 2:
The probability that the event Ava gets a snickers is 9/21 since there are 9 snickers out of a total of 21 candies.
After Ava has taken her snickers, there are 8 left so the probability that the event Madison gets a snickers is 8/20. 20 because there 20 candies left after Madison took a snickers.
The compute the probabiLity that both events occur is found by:
`P_a & P_b = P_a * P_b`
where `P_a` is the probablity of the event Ava gets a snicker and ` P_b` is probablity of the event Madison gets a snicker . Plug in the numbers:
`P_a & P_b = 9/21 * 8/20`
If you were doing the problem without a calculator, it would pay to notice the chance to divide before multiplying. That makes the numbers smaller and easier to handle.
`P_a & P_b = 3/7 * 2/5`
`P_a & P_b =6/35`
Problem 3:
In general, if you start with `n` cells there are `n*2^d` cells after `d` divisions.
The cells divide every 12 hours so there are 2 divisions per day.
They divide for 29 days so there are a total of `2*29` or 28 divisions.
The colony began with 9 cells.
The answer is computed by evaluating `9*2^58`.
Problem 4:
You can represent the 3 clothing choices with 3 slots shown below

She has 7 pairs of pants and 7 skirts so she has 14 choices for the first slot.
She has 11 pairs of shoes so she has 11 choices for the second slot.
She has 12 blouses so she has 12 choices for the third slot.
Populate the slots as shown:
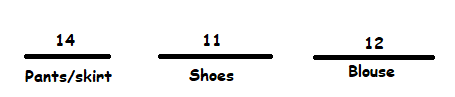
Since the choices are independent of each other, you multiply the 3 numbers and get 1848.
Problem 5:
`Probability = \text(The number of ways for the desired event to occur)/ \text(The total number of outcomes )`
In class, we use the shorthand ...
`Probability = \text( desired )/ \text( total )`
The train has 10 seats of which 3 are broken. The total number of ways the conductor could mark the form is ` \ _10C_3`. We use 10 Choose 3 instead of ` \ _10P_3` because the order that the broken seats are marked doesn't matter; the form will look identical.
Of all the ways the conductor can mark the form, there's exactly one way that correctly identifies the broken seats so the number of ways to get the desired outcome is `1`.
The answer is found by computing
`Probability = 1 / ( \ _10C_3)`
Remember that the formula for `\ _nC_r` is :
`\ _nC_r = (n!)/((n-r)!r!)`
For this problem, the form is:
`\ _10C_3 = (10!)/((10-3)!3!)`
If you didn't have a calculator you can divide before multiplying by observing that
`10! = 10 * 9 * 8 *7!` and `3! = 3*2*1`
substituting:
`\ _10C_3 = ( 10 * 9 * 8 *7!)/(7!*6)` . The `7!`s cancel out because `(7!)/(7!) = 1` so:
`\ _10C_3 = ( 10 * 9 * 8 )/( 6)` . Observe that `6 =2*3`, `9=3*3` and `10=2*5` so:
`\ _10C_3 = ( 2*5 * 3*3 * 8 )/( 2*3)` The 6 is completely canceled leaving:
`\ _10C_3 = ( 5 * 3 * 8 )/1 `
So there are 120 ways of marking t the 3 broken seats in a 10 seat car.
`Probability = 1 / (120)`
The answer in scientific notation is `8.33*10^(-3)`
Pro Tips!
- When you calculate `\ _nC_r` or `\ _nP_r` , the correct answer is always a positive integer. If your calculator gives you a negative or fractional answer, you've made a mistake.
- Probability answers are always a fraction between 0 and 1 inclusive.That's because
the desired number of outcomes can't be bigger than the total number of outcomes.
if you had written 120 as your answer you should see immediately that 120 was not the asnwer because 120 is bigger than 1.
Mathcounts rules
- Mathcounts is finicky about formats. `1/120` is the correct number but in the wrong format. Answer in the wrong format and the answer is marked as wrong.
- Similarly, if the the answer requires 3 significant digits, answering with `8.3*10^(-3)` or `8.333*10^(-3)` would also be marked as wrong. The former is 2 significant digits and the later is 4 significant digits whereas the required format was for 3 significant digits.